在机器学习中，常见到两个函数名称： sigmoid 和 softmax 。前者在神经网络中反复出现，也被称为神经元的激活函数；后者则出现在很多分类算法中，尤其是多分类的场景，用来判断哪种分类结果的概率更大。

本文主要介绍这两个函数的定义、形态、在算法中的作用，以及两个函数之间的联系。

1. Sigmoid函数

1.1. 函数定义

sigmoid 函数是一类函数的统称，常见的 sigmoid 函数有： \(y=\frac{1}{1+e^{-x}}\) 。它有时也被称为 S函数 ，是因为它的图像显示出来是 S形 的。

x = np.linspace(-10, 10, 100)
y = 1 / (1 + np.exp(-x))

plt.figure(figsize=(6, 4))
plt.plot(x, y)
plt.title("S-函数")
plt.grid(True)

plt.show()

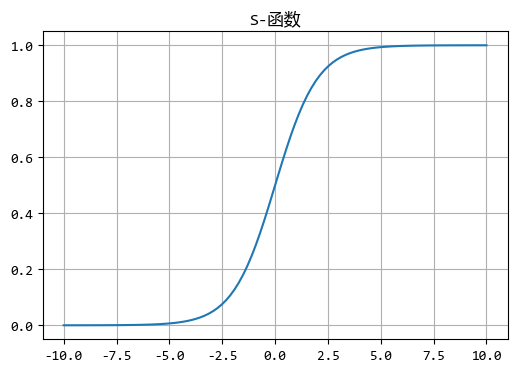
从图形可以看出， S函数 的输出会控制在一个有限的范围内（上面的函数是0~1之间），这个特性使得它非常适合表示概率或者用于二分类问题的输出层。

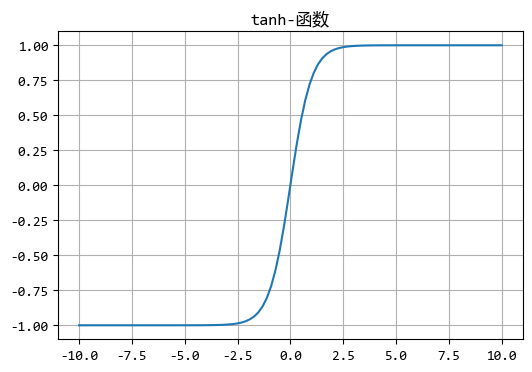
注意， sigmoid 函数的输出并不是一定要在区间 (0,1) 中，比如还有个常用的 S函数 ： \(tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\) ，它的的输出区间是 (-1,1) 。

1.2. 应用场景

sigmoid 函数的主要使用场景有：

1. 逻辑回归算法： sigmoid 函数可用于将线性回归模型的输出转换为概率值，从而用于二分类问题。模型输出的概率值表示了样本属于某一类的可能性。
2. 神经网络的激活函数：它帮助神经网络学习复杂的决策边界，通过非线性转换增加模型的表达能力。
3. 门控机制：在 LSTM （长短期记忆网络）等循环神经网络中， sigmoid 函数（或其变体）被用作门控机制的一部分，以控制信息的流动。

sigmoid 函数在机器学习和早期的深度学习中扮演着重要的角色，尤其是在处理二分类问题和作为神经网络中的激活函数时。随着深度学习的发展，其他激活函数因其更优越的性能而逐渐取代了 sigmoid 函数在某些场景下的地位。

2. Softmax函数

2.1. 函数定义

接下来介绍 softmax 函数， softmax 函数是一种在机器学习和深度学习中广泛使用的函数，特别是在处理多分类问题的场景中。而上面介绍的 sigmoid 函数更多应用在二分类场景。

softmax 函数的主要作用是将一个 K维 向量（通常表示每个类别的原始预测分数）转换成一个元素范围都在 (0, 1) 之间 K维 向量，并且所有元素的和为 1 。这段话有点抽象，举个例子来说，比如有一个3维向量： \((x_1,x_2,x_3) = (3,1,-2)\) ，其中每个元素的值都不在区间 (0, 1) 中，所有元素的和也不是 1 。

那么， softmax 函数是如何转换的呢？首先，求出各个元素的 exp 的和： \(m=e^{x_1}+e^{x_2}+e^{x_3}\) 。然后，将向量 \(x\) 转换为向量 \(y\) : \((y_1,y_2,y_3)= (\frac{e^{x_1}}{m},\frac{e^{x_2}}{m},\frac{e^{x_3}}{m})\approx(0.876,0.118,0.006)\) 转换之后的 \(y\) 向量每个元素的值都在区间 (0, 1) 中，并且所有元素的和为 1 。

softmax 函数也可以绘制图形。

from mpl_toolkits.mplot3d import Axes3D

def softmax(x0, x1, x2):
    m = np.exp(x0) + np.exp(x1) + np.exp(x2)
    return np.exp(x0) / m, np.exp(x1) / m, np.exp(x2) / m

count = 30
x0 = np.linspace(-10, 10, count)
x1 = np.linspace(-5, 5, count)

y = np.zeros((count, count, 3))
for i0 in range(count):
    for i1 in range(count):
        y[i1, i0, :] = softmax(x0[i0], x1[i1], 1)

xx0, xx1 = np.meshgrid(x0, x1)
plt.figure(figsize=(10, 4))

ax1 = plt.subplot(1, 2, 1, projection="3d")
ax1.plot_surface(xx0, xx1, y[:, :, 0], color="g")
ax1.set_xlabel("$x_0$", color="g")
ax1.set_ylabel("$x_1$", color="g")
ax1.set_zlabel("$y_0$", color="g")

ax2 = plt.subplot(1, 2, 2, projection="3d")
ax2.plot_surface(xx0, xx1, y[:, :, 1], color="r", cstride=1)
ax2.set_xlabel("$x_0$", color="r")
ax2.set_ylabel("$x_1$", color="r")
ax2.set_zlabel("$y_1$", color="r")
ax2.zaxis.labelpad=-1

plt.tight_layout()
plt.show()

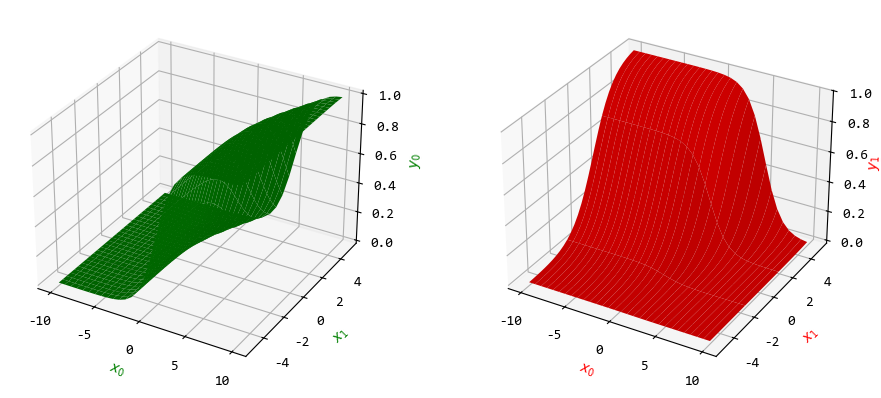
从图中可以看出， \(y_0,y_1\) 被映射到区间 (0, 1) 中。

2.2. 应用场景

softmax 函数可以应用在：

1. 多分类问题：它是处理多分类问题时的标准输出层激活函数。能够将模型的原始输出（通常是线性层的输出）转换为概率分布，便于后续使用交叉熵损失函数进行训练。
2. 神经网络的输出层：在构建用于分类任务的神经网络时，常被用作输出层的激活函数。特别是在卷积神经网络（ CNN ）、循环神经网络（ RNN ）及其变体中用于生成最终的类别预测。
3. 强化学习：在某些强化学习场景中，可用于将Q值（即动作的价值估计）转换为选择每个动作的概率，从而实现基于概率的动作选择策略。
4. 自然语言处理：用来计算注意力权重，这些权重决定了模型在处理输入时应该给予哪些部分更多的关注。

softmax 函数是机器学习和深度学习中处理多分类问题、生成概率分布和进行概率决策的重要工具。

3. 两者的联系

最后，再分析下这两个函数的关系。根据前面的介绍， sigmoid 函数适合二分类问题， softmax 函数适合多分类问题。那么， sigmoid 函数会不会是 softmax 函数的一个简化版本呢？

假设一个只有两个变量的 softmax 函数，那么其中 \(y_0=\frac{e^{x_0}}{e^{x_0}+e^{x_1}}\) ，分子分母同时乘以 \(e^{-x_0}\) 可得： \(y_0=\frac{e^{x_0}e^{-x_0}}{e^{x_0}e^{-x_0}+e^{x_1}e^{-x_0}}=\frac{e^{x_0-x_0}}{e^{x_0-x_0}+e^{x_1-x_0}}=\frac{1}{1+e^{-(x_0-x_1)}}\) 。假设 \(y=y_0, x = x_0-x_1\) ，可得： \(y=\frac{1}{1+e^{-x}}\) ，这就是一个典型的 sigmoid 函数。

因此，我们可以认为 softmax 函数是将 sigmoid 函数扩展到多变量之后而得到的。