
我们提供安全,免费的手游软件下载!
我们在上一篇博客 《概率论沉思录:定量规则》 中介绍了合情推理 [1][2] 的定量规则,即:
根据乘法规则和加法规则,可以导出广义加法规则:
\(p(A + B \mid C) = p(A\mid C) + p(B\mid C) - p(AB\mid C)\)
;
根据加法规则和无差别原则,我们又得到了
伯努利坛子规则
:如果有
\(N\)
个除标号外各方面都相同的球,命题
\(A\)
被定义为在任意的
\(M\)
个球的子集上为真(
\(0\leqslant M \leqslant N\)
),在其补集上为假,我们有:
事实上,只需要以上规则就可以导出概率论中的许多结论。接下来我们来看看我们的推理机器人是如何依据这些规则完成推理,并得到许多经典的结论的。
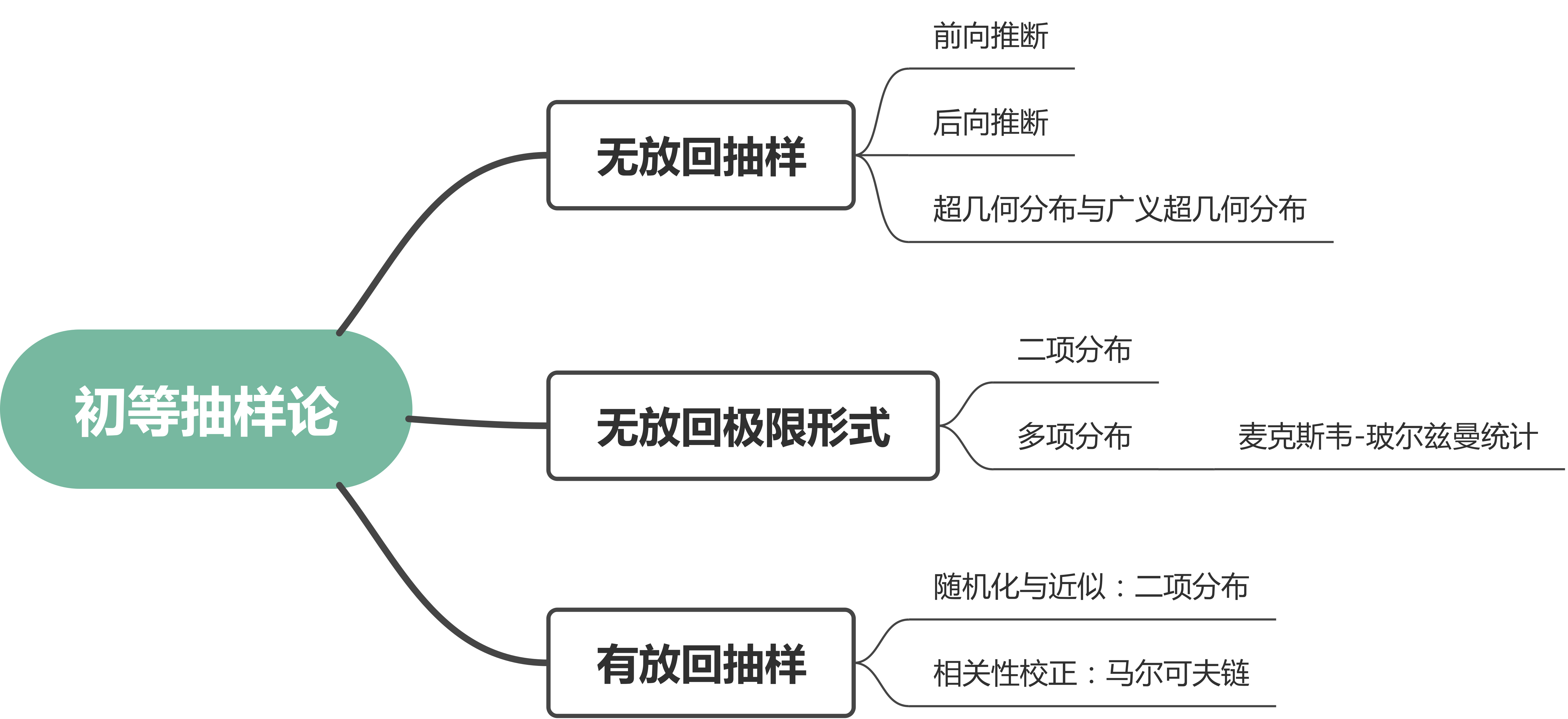
首先,我们做一个术语约定,我们称从坛子里抽一次球为一次 试验(trial) , \(n\) 次试验构成一次 实验(experiment) 。我们接下来会先考察 无放回抽样(sampling without replacement) 实验,也即从有 \(N\) 个球的坛子里无放回地抽 \(n\) 个球,我们会发现实验结果服从超几何分布/广义超几何分布。接着,我们会讨论前向推断和后向推断两类问题。然后,我们会研究无放回抽样的极限形式,这将导出二项分布/多项分布。关于多项分布,我们还会进一步讨论统计力学中的麦克斯韦-玻尔兹曼统计。
最后,我们会考察更复杂的 有放回抽样(sampling with replacement) 实验,也即从有 \(N\) 个球的坛子里无放回地抽 \(n\) 个球。注意,与许多人认为的相反,我们认为无放回抽样更复杂,因为我们需要考虑大量的额外背景信息并进行分析。之所其二项分布的数学形式更简单,是由于我们做出了随机化的额外假设导致的,我们所得到的只是个近似的结果。最后,我们会对有放回抽样的近似结果做进一步的相关性校正,这将得到一个马尔可夫链模型。
本文的思维导图如下所示:
首先,我们通过以下命题的定义来进一步明确无放回抽样实验的定义:
对于第 \(k\) 次( \(1 \leqslant k \leqslant N\) )抽取而言,根据背景信息 \(B\) ,取出红球和取出白球是互斥的,故有 \(\overline{R_k}=W_k\) ( \(\overline{W_k}=R_k\) ),且根据加法规则满足 \(p(R_k\mid B) + P(W_k\mid B) = 1\) 。
特别地,对于第1次抽取而言,可以直接结合伯努利坛子规则得:
让我们重申一次:上述两个概率赋值不是对坛子与其容纳物的任何物理属性的断言,而是在抽取前对机器人 知识状态 的描述(初始时的知识状态即背景信息 \(B\) )。试想,如果机器人初始的知识状态与 \(B\) 不同,例如它知道坛子中红球和白球的实际位置,或者它不知道 \(N\) 与 \(M\) 的实际值,那么它对 \(R_1\) 和 \(W_1\) 的概率赋值将会不同,但是坛子本身的物理属性是一样的。
而当我们询问第二次抽取相关的概率时,机器人的知识状态就会出现变化。例如,问前两次取出的都是红球的概率 \(P(R_1R_2\mid B)\) 是多少?我们使用乘法规则将其拆解为分步判定:
注 事实上,这里我们默认了按照时间顺序,也即先 \(1\) 后 \(2\) ,这就是所谓的前向推断;但是在逻辑上(而非物理因果上)我们也可以定义先 \(2\) 后 \(1\) ,这叫后向推断。具体区别我们后面会进行详述。就是要注意我们一直说的是“分步判定”而非“分步决策”,就是因为我们只考虑逻辑上的先后而不考虑时间上的先后(逻辑上的先后可能和时间符合,也可能不符合)。
注意在判定最后一项时,机器人需要再次应用伯努利坛子规则,不过必须考虑到在第一次抽取中已经取走了一个红球,所以:
这样继续进行下去,重复应用伯努利坛子规则,则前 \(r\) 次取出的都是红球的概率 \(P(R_1R_2\cdots R_r\mid B)\) 可以表示为:
这里 \((M)_r=M(M-1)\cdots (M-r+1)\) , \((N)_r=N(N-1)\cdots (N-r+1)\) ( \(r\leqslant M\) )(该记号来自William Feller的书 [3] ,我觉得不错故用之)。对于白球而言只需要把 \(M\) 换成 \(N-M\) ,然后把 \(r\) 换成 \(w\) 即可,即 \(P(W_1W_2\cdots W_w\mid B) = \frac{(N-M)_w}{(N)_w}\) 。
现在,我们要问:如果我已知前 \(r\) 次取到的都是红球,那么后 \(r+1, r+2, \cdots, r+w\) 次取到的都是白球的概率是多少?此时,机器人已经知道了 \(r\) 个红球已拿出,也即总共还剩下 \(N-r\) 个球了(当然,白球数量还是 \(N-M\) ),那么:
利用乘法规则,可得在 \(r+w\) 次抽取中,先抽中 \(r\) 个红球,再抽中 \(w\) 个白球的概率为:
事实上,即使红球和白球的取出以其它顺序进行交错,所得结果也是这个。也就是说,上式给出了以 任意指定顺序 \(S_l\) (比如指定 \(RRRW\cdots\) , \(RWRW\cdots\) 等序列其中一种)取出 \(r\) 个红球与 \(w\) 个白球的概率 \(P(S_l\mid B)\) 。因为不管以怎样的顺序交错地取出红球和白球,分母都是从 \(N\) 跑到 \(N-r-w+1\) ,而分子中红球数总得从 \(M\) 扣到 \(M-r+1\) ,白球数也总得从 \(N-M\) 扣到 \(N-M-w+1\) (不论其以什么顺序来扣)。
接下来,我们要问:以任意顺序取出 \(r\) 个红球与 \(w\) 个白球的概率是多少?任何一个红球和白球出现的指定序列 \(S_l\) 都是互斥的事件,因此我们根据加法规则来求和(注意和的每一项 \(P(S_l\mid B)\) 都是相同的):
式子中的组合数 \(\binom{r+w}{r}\) 为在 \(r+w\) 次抽取中取出 \(r\) 个红球的可能序列的数量,我们称其为事件「在 \(r+w\) 次抽取中取出 \(r\) 个红球」的 重数(multiplicity) 。事件的重数可能具有多种形式,这里的形式为 二项式系数(binomial coefficient) ,我们后面还会看到更多类型的重数。
注 这里有读者可能会细究,既然我们的球是有标号的,那么所有的可能序列数为啥不是 \((r+w)!\) 呢?请注意,尽管球有标号,但我们的机器人在每轮抽球即计算 \(P(R_1\mid B), P(R_2\mid R_1B), \cdots\) 时并没有指定抽哪个红球或白球(也即每轮计算的概率本身就包含了各种标号的概率,如 \(P(R_1\mid B)=P(A_4 + A_6 + A_7 \mid B)\) ,这里 \(4, 6, 7\) 为所有红球的标号),乃至最后计算 \(P(S_l\mid B)\) 时也并没有指定要取出哪些红球和白球,故这里不是 \((r+w)!\) 。
利用事实 \((M)_r=\frac{M!}{(M-r)!}\) , \((N)_r=\frac{N!}{(N-r)!}\) , \(\binom{r+w}{r}=\frac{(r+w)!}{r!w!}\) 来进行化简,我们就得到了 超几何分布(hypergeometric distribution) 的定义:
注意,概率只在 \(r\leqslant n\) 且 \(r\leqslant M\) 时有定义。虽然如此,当 \(b>a\) 时 \(\binom{a}{b}=0\) ,因此当 \(r > n\) 或 \(r > M\) 时,上式会给出 \(0\) 。因此,只要规定 \(r > 0\) 且把 \(h=0\) 的事件解释为不可能事件就行了。
进一步推广,假设坛子里面有 \(c\) 种不同颜色的球,颜色 \(c\) 的球有 \(N_c\) 个,则在 \(n=\sum_{i=1}^c r_i\) 次抽取中取出“ \(r_1\) 个颜色1的球, \(r_2\) 个颜色2的球,..., \(r_c\) 个颜色 \(c\) 的球”的概率是 广义超几何分布 :
一般地,对于概率分布 \(p(x_1, \cdots, x_n\mid B)\) ,其中 \(x_k\) 表示第 \(k\) 次的试验结果,并且可以取不止两个值(红色和白色),比如, \(x_k=1, 2, \cdots, c\) 标记 \(c\) 种不同的颜色。如果该概率在 \(x_k\) 的任何排列下都是不变的,则它仅取决于表示“结果 \(x_k=1\) 出现了多少次, \(x_k=2\) 出现了多少次等等”的样本数 \((n_1,\cdots, n_c)\) 。这种分布称为 可交换的(exchangeable) 。我们这里的超几何分布/广义超几何分布就是可交换的。
超几何分布具有以下两种较为显著的 对称性(symmetry) :
对称性1:关于 \(M\) 和 \(n\) 的对称性
超几何分布在交换 \(M\) 和 \(n\) 时值不变:
这也就意味着当总球数为100时,无论我们是从包含50个红球的坛子里抽取10个球,还是从包含10个红球的坛子里抽取50个球,再取出的样本里找到 \(r\) 个红球的概率是相同的。
对称性2:关于峰值的对称性
如果我们交换 \(M\) 和 \(N-M\) ,并同时交换 \(r\) 和 \(n-r\) ,那么实际上是交换了“红色”和“白色”的定义,所以分布不变,即
除了以上两种对称性之外,超几何分布还有两种在直观上并不显而易见的对称性,其中一种为关于 \(k\) 的对称性。
隐藏对称性1:关于 \(k\) 的对称性
现在我们想问机器人第2次取出红球的概率 \(P(R_2\mid B)\) 是多少?此时我们是否还能够像计算 \(P(R_2\mid R_1B)\) 那样利用伯努利坛子规则呢?我们虽然已知第二次抽时只剩下 \(N-1\) 个球,但是红球数 \(M\) 是不确定的(或为 \(M\) 或为 \(M-1\) )。因此,伯努利坛子规则的前提就不存在,看起来问题是不确定的。
然而,问题其实是确定的。以下是我们在概率计算中使用实用技术的第一个例子,它将一个命题分解为更简单的子命题(当然,这里的子命题选择必须恰当,不然就会和上一篇博客提到的南极企鹅个数一样无用)。机器人知道 \(R_1\) 或 \(W_1\) 是真的,因此使用布尔代数可以得到
那么我们应用加法规则和乘法规则就可以得到
由于 \(P(R_1\mid B)=\frac{M}{N}, P(R_2\mid R_1B)=\frac{M-1}{N-1}\) ,且 \(P(W_1\mid B)=\frac{N-M}{N}, P(R_2\mid W_1B)=\frac{M}{N-1}\) ,所以
复杂性消失了!第二次抽出红球的概率居然和第一次相同!事实上,我们继续验证,可以得到 \(R_3, R_4, \cdots\) 都为 \(M/N\) 。事实上, 如果不知道任何其它次抽取的结果,机器人在任何一次抽取中抽中红球的概率总与伯努利坛子规则相同 ,也即:
这是第一个并不显而易见的对称性。后面我们会看到,这是一个更一般结果的特例(证明我们往后放,参见 3.2节 相关性校正:马尔可夫链 )。
我们前面提到超几何分布上可交换的,也即满足概率分布 \(p(x_1, \cdots, x_n\mid B)\) 在 \(x_k\) 的任何排列下都是不变的。那么要保证这种可交换性,必然要求每次抽取对其它次抽取施加相同的影响,无论其时间顺序或在序列中的位置如何。这并不限于超几何分布,对于任何可交换分布都是正确的。
让我们定量地计算这一影响。假设
\(j
上式实际上为 \(2^{j-1}\times 2^{k-j-1}=2^{k-2}\) 个合取命题的逻辑和(也即我们提到过的析取范式,DNF),其中每一个合取命题代表诸如 \(W_1R_1W_3\cdots R_j \cdots R_k\) 的完整序列。
上式看起来比较难以处理,因为 \(R_j\) 、 \(R_k\) 之间还相隔了许多次抽取。但是,我们已经知道,在给定 \(B\) 的情况下,任何一个序列的概率都与其红球和白球的出现顺序无关。因此,我们可以变换序列,将 \(R_j\) 移动到第1个位置,将 \(R_k\) 移动到第2个位置。此时:
此时,最后一个等式成立的理由是已知在第1次和第2次之后“摸到红球或白球”并没有为我们提供背景信息 \(B\) 之外的更多信息。
这样,我们就有
根据乘法规则,对所有 \(j < k\) ,有
这种已知第 \(j\) 次的抽取结果,对第 \(k\) 次( \(k > j\) )抽取结果的概率所进行的推断,我们称之为 前向推断(forward inference) 。我们惊奇地发现, \(P(R_k\mid R_jB)=(M-1)/(N-1)\) 意味着对于前向推断而言,我们的伯努利坛子规则仍然适用,只不过初始条件变化了而已(已知从罐子里面取出了一个红球)。最后,问题规约为从有 \(N-1\) 个球的坛子(其中有 \(M-1\) 个是红球)里抽球。
从上一节我们可以看出,当机器人在计算第 \(k\) 次抽取红球的概率时,显然与之前抽取的结果信息是相关的(例如, \(P(R_k\mid B) \neq P(R_k\mid R_jB)\) ),这是因为更早的抽取结果会在物理上影响第 \(k\) 次抽取时坛子中的红球数量 \(M_k\) 。这种前向推断的结果是符合我们物理直觉的。
那么第 \(k\) 次推断的结果是否与后面某次抽取的结果相关呢?咋一看不太可能,因为之后抽取的结果在物理上不会影响 \(M_k\) 的值。比如,彭罗斯(Penrose)在著名统计力学文献《Foundations of Statistical Mechanics》就将“当前事件的概率只能取决于前面发生的事件,而不取决于后面发生的事件”做为基本公理。作者认为这是“因果律”(Causality)的必要物理条件。
但是正如我们已经声明的,我们只关心 逻辑关系 ,而逻辑关系可能与 物理因果作用 相关,可能无关。有一个极端的例子可以说明为什么后面发生的事件的信息与前面发生的事件有关。假设坛子里面只有一红一白两个球,如果机器人知道第2次抽取时抽中红球,那么它会直接将第一次抽中红球的概率判为0: \(P(R_1\mid R_2B)=0\) ,而不再是 \(1/2\) 。
隐藏对称性2: \(k\rightarrow j\) 与 \(j\rightarrow k\) 的对称性
接下来让我们来推导更一般的结论。根据乘法规则,我们有
我们在1.1节中已经知道,对于所有的 \(j\) 和 \(k\) 都有 \(P(R_j\mid B) = P(R_k\mid B)=M/N\) ,那么必要就有
这说明后面的抽取结果与前面的抽取结果具有完全相同的作用。这是因为,尽管第 \(k\) 次抽取后的抽取不会物理地影响坛子中的红球数量 \(M_k\) ,但后面抽取结果的 信息 与前面抽取结果的信息对第 \(k\) 次抽取的 知识状态 具有相同的影响。这是第二个并不显而易见的对称性。
注 这一结果可能会让某些对“概率意义”持有思想的流派不安。尽管人们普遍认同逻辑蕴含关系与因果关系不同,但是很倾向于将概率 \(P(A\mid B)\) 解释为 \(B\) 对 \(A\) 的某种部分因果作用。这不仅在前面提到的彭罗斯的著作中很明显,在哲学家卡尔·波普尔(Karl Popper)对概率做出的 倾向性(propensity) 解释中也很明显。波普尔将概率看做是一集可重复的条件所固有的客观倾向。他认为在量子理论中人们在客观的纯统计解释和基于不完全知识的解释之间摇摆,而他的倾向性解释可以避免使用不完全知识的解释。我们认为他完全错了, 不完全的知识是科学家拥有的唯一工作材料 。
但是,这并不意味着我们禁止引入“倾向”或“物理因果”的概念,这里的关键是无论是否存在倾向,逻辑推断都是适用且有用的。事实上,在所有科学中,逻辑推断都具有更普遍的适用性,因为物理作用只能沿时间前向传播,但是逻辑推断在前后两个方向上都可以传播。考古学家发现的一件人造物能改变他对几千年前的事件的认识,夏洛克·福尔摩斯的推理旨在根据现有的证据推断过去发生的事件。其中的关键在于, 我们对任何现象做出的最佳科学推断,都必须参考我们拥有的所有相关信息,无论这些信息是在现象发生之前还是之后的 。
接下来让我们定量地计算这一影响。我们之前在计算前向推断时,已经得到 \(P(R_jR_k\mid B) = \frac{M(M - 1)}{N (N - 1)}\) 。请注意,乘法规则对后向推断也同样适用,于是对所有 \(j < k\) ,有
我们惊奇地发现, \(P(R_j\mid R_kB)=P(R_k\mid R_jB)=(M-1)/(N-1)\) 。说明已知之前抽了个红球和已知之后抽了个红球有同样的作用。这是因为,如果机器人知道后面会取出红球,那么实际上必须将坛子中的红球之一“搁置”起来,以使这成为可能。于是,本可以在前面取出的红球数就少了一个。
然而,这里的直观理解当问题更复杂时可能会带来一定的误导。比如,我们假设机器人在后面的抽取中至少会取出一个红球,但不知道是哪一(几)次。也就是说,新信息可以用布尔代数的命题形式表示为 \(R_{\text{later}}\equiv R_{k+1} + R_{k+2} + \cdots R_n\) 。我们可能会凭借自己直觉认为 \(P(R_k\mid R_{\text{later}}B) < P(R_k\mid B)\) ,然而事实却出人意料,应该是: \(P(R_k\mid R_{\text{later}}B) > P(R_k\mid B)\) 。
这是为什么呢?因为在之前的 \(P(R_j\mid R_kB)=\frac{M-1}{N-1}\) 的情况里,信息 \(R_k\) 可让第 \(j\) 次可抽的红球数减1,也可以让第 \(k\) 次可抽的总球数减1。但是,在 \(P(R_k\mid R_{\text{later}}B)=\frac{M-(1 + p_\delta)}{N-\Delta}\) (其中 \(\Delta, \delta > 1\) , \(p_{\delta}\) 为 \([0, 1]\) 之间的小数,表示后面抽中 \(\delta\) 个红球的概率)的情况里,第 \(k\) 次可抽的红球数虽然也是减掉大约1,但是第 \(k\) 次可抽的总球数却需要减去 \(\Delta > 1\) (因为它向机器人说明以后还要进行 \(\Delta\) 次抽取,还要减去 \(\Delta\) 个球)。
尽管数学形式上有些复杂,但超几何分布是一个概念上非常清晰、简单的问题引起的。为了引入一个数学上更简单但概念上更困难的问题,我们先来研究超几何分布的一种极限形式。
超几何分布之所以复杂,是因为它考虑了坛子内容的不断变化,知道任何一次抽取的结果都会改变其它次抽中红球的概率。但是,如果坛子中的球数 \(N\) 比取出的球数 \(n\) 大得多( \(N\gg n\) ),那么该概率的变化很小。在极限 \(N\rightarrow + \infty\) 时,我们会得到一个更简单的结果,直接没有这种依赖性。为了验证这一点,我们将超几何分布分子分母同乘 \(N^n\) 并配凑为:
第一个因子是
取极限 \(N\rightarrow + \infty, M\rightarrow +\infty, M/N\rightarrow f\) ,我们有
类似地,我们有
将这些极限乘起来(原则上我们应该采用乘积的极限而非极限的乘积,但这些因子各自都有极限,故可以这样搞),就得到了超几何分布的极限—— 二项分布(binomial distribution) :
和超几何分布相比,事件「在 \(n\) 次抽取中取出 \(r\) 个红球」的重数仍然是 \(\binom{n}{r}\) ,只不过生成每一个指定序列的概率取了极限,变为了 \(f^r (1 - f)^{n - r}\) 。
对广义超几何分布执行类似的极限过程,可以证明:如果所有 \(N_i\rightarrow +\infty\) ,且满足 \(N_i / \sum_{j=1}^c N_j\rightarrow f_i\) ,那么广义超几何分布就会变成 多项分布(multinomial distribution) :
其中 \(n\equiv \sum_{i=1}^c r_i\) 。此时,事件「在 \(n\) 次抽取中取出 \(r_1\) 个颜色1球, \(r_2\) 个颜色2的球,..., \(r_c\) 个颜色 \(c\) 的球」的重数为 \(n! / (r_1!\cdots r_c!)\) 。这种形式的重数叫做 多项式系数(binomial coefficient) 。
多项式系数的应用非常广泛。比如在统计力学中,我们常常需要计算把 \(n\) 个不可区分的粒子(球)划分到 \(c\) 个相空间的小区域(盒子)中的概率。这种概率分布有两种计算方法,其中一种是 麦克斯韦-玻尔兹曼统计 (这里所用的“统计”一词是物理中的术语),其计算方法为:
这里 \(f= 1 / c\) 。这里的思想和我们之前模球很相似, \(f^n\) 可视为先按照球可区分(带标号)的情况所计算的每一种划分方式的概率,乘上重数 \(n! / (r_1!r_2!\cdots r_c!)\) 得到同盒子内的球不可区分(同一个盒子内的球可任意排列)的概率。不过,这个统计法则只在经典力学背景下适用。我自己的直观理解方式是,虽然我们假设球不可区分,但这些球依然具有标号,所以我们才能先按照可区分的情况计算概率然后再乘以重数。但是在量子力学的基本假设下,许多粒子(如电子、质子、中子等)常常是完全不可区分的,我们称为全同粒子(identical particles),假定所有球带有标号就不再适用了。
注 还有一种适用于量子力学背景下的计算方法称为 玻色-爱因斯坦统计 ,只考虑那些可区分的划分方式,且每一个可区分的划分方式都赋以相等的概率。根据组合数学知识我们知道, \(n\) 个不可区分的球划分到 \(c\) 个可区分的盒子的划分方式共有 \(\binom{n + c - 1}{n}\) 种,于是每一种划分方式的概率为:
这个假设对于所有的玻色子(如光子、原子和原子核等)都是正确的。玻色子可以是基本粒子(如光子),也可以是复合粒子(如原子、原子核)。由偶数个费米子组成的复合粒子都是玻色子。玻色子的自旋为整数。
以上两种分布的分歧在于究竟 怎么给样本空间赋概 。麦克斯韦-玻尔兹曼分布可视为给(可区分划分方式构成的)样本空间中的 \(\binom{n + c - 1}{n}\) 个样本点按照多项式系数的重数来赋概,用扔硬币来类比就是扔两次硬币的样本空间{2正, 1正1反, 2反}中的样本点分别赋概 \(1/4, 1/2, 1/4\) (不过注意我们这里的为“量子硬币”,也就是两个硬币具有全同性,正反和反正不可区分)。而玻色-爱因斯坦分布对每一个样本点赋概 \(1/3\) 。玻色最开始做出这个发现时其实就源于把扔两次“量子硬币”进行了(按照我们常识来看)“错误的”赋概,赋成了 \(1/3\) ,然后居然发现和黑体辐射相吻合!但是他投稿的时候论文被拒了。最后他给爱因斯坦写信,爱因斯坦马上意识到这个问题不简单,开始进行研究,最后提出了一种现在被称为玻色-爱因斯坦统计的新的统计方式。这其实也证明了一个观念,那就是 不可能在毫无知识状态的情况下对样本空间赋概 ,频率派要求定义样本空间的麻烦之处也在此,尽管频率派常拿先验来攻击贝叶斯派,然而其样本空间的赋概却是用到了先验知识的。
最后,还有一种适用于量子力学背景下的方式是假设2个或多个球在同一个盒子中是不可能的(这里假定 \(n\leqslant c\) ),且满足该条件的所有可区分划分方式具有相同的概率,每一种划分方式都相当于 \(c\) 个盒子中某 \(n\) 个各含一个球,也就是说,每一种划分方式相当于从 \(c\) 个盒子中选取 \(n\) 个,这种计算方式称为 费米-狄拉克统计 :
这个模型可以应用在费米子(如电子、质子和中子等)上。费米子可以是基本粒子(如电子),也可以是复合粒子(如质子、中子)。任何由奇数个夸克或轻子组成的复合粒子都是费米子。费米子的自旋为半整数。
到目前为止,我们仅考虑了无放回抽样的情形。而这对于许多实际情况是合适的,比如在质量控制过程中我们“抽取一个球”可能是从一箱类似的产品(例如电灯泡)中抽取一个,并对其进行检测。我们很难想象在实际情况中能再次“抽取同一个球”。
但是,如果我们假设检测的破坏性较小,从坛子中抽取球并记录球的“颜色”(即相关属性)后,可以将其放回坛子中再抽下一个球。这种有放回抽样的情况在概念上要复杂得多,但是我们可以通过做出一些假设使其在数学上比无放回抽样更简单。对于我们之前提到的连续抽取两个红球的概率,用 \(B^{\prime}\) 表示与以前相同的背景信息(除了有放回外),根据乘法规则我们仍然有下列等式:
第一个因子仍然是 \(M / N\) ,但第二个因子呢?
回答这个问题其实很困难,因为需要进行大量的额外分析,且要求背景信息 \(B^{\prime}\) 需要包含足够多的信息,比如:我们放回坛子的那个红球会怎样?如果我们将其放回的时候丢在其它球的上层,那么在下次抽取的时候它会比坛子中其它位置的球更有可能被取出。事实上,这动摇了我们计算的全部基础:我们的伯努利坛子规则不再适用!因此,即使掌握了这些信息,整个问题可能根本就无法下手,所产生的计算代价也可能是巨大的。但是这个问题在原理上并非不能解决,只是过于复杂,这该怎么办呢?
在概率论中,有一个非常巧妙的技巧可以解决过于困难的问题。无论问题多困难,我们都可以通过以下方式解决:
具体在有放回抽样的情况下,我们采用以下策略:
注 随机化通常会产生对正确解的有用近似。因为摇动不会使结果变得“随机”(random),因为该术语在做为现实世界的属性时基本上没有意义,它没有适用于现实世界的明确定义。认为“随机性”(randomness)是自然界中存在的某种真实性质,是思维投射谬误的一种形式,这相当于在说:“我不知道详细的原因(认识论角度),所以大自然也不知道(本体论角度)”。事实上,摇动不会以任何方式影响大自然的运作,只能确保没有人(human)能对结果施加主观影响。因此,没有人会因为随后“固定的”结果被指控(比如美国某电视节目中出现的从鱼缸里取数来确定服役顺序)。
但是,我们必须要坦诚地承认自己做了什么:我们不是在解决实际问题,而是在做出现实的妥协,并对近似答案感到满意。持柏拉图主义的数学家可能认为现实世界是对抽象数学的近似,但我们的观点恰恰相反:抽象数学才是对现实世界的近似。数学家们常常使用语言暗示他们是在证明真实世界的性质,但我们认为:没有任何数学模型可以捕获现实世界中所有与之相关的情况。任何认为自己在证明现实世界性质的人都是思维投射谬误的受害者。
现在回过头来看,我们对等式右侧的第二个因子 \(P(R_2\mid R_1 B^{\prime})\) 可以给出怎样的答案?按我们原本的观念来看,在第二次抽取时红球的概率 \(P(R_2\mid R_1 B^{\prime})\) 显然不仅取决于 \(N\) 和 \(M\) ,还取决于已经取出并放回红球的事实。但是后者的依赖非常复杂,以至于在现实中无法考虑。因此,我们采取新的策略:摇动坛子进行“随机化”,然后宣布 \(R_2\) 和 \(R_1\) 不相关: \(P(R_2\mid R_1 B^{\prime}) = P(R_2\mid B) = M / N\) 。以此类推,每一次试验中取出红球的概率都为 \(M/N\) 。
这再次重复了我们之前提到的隐藏对称性1:关于 \(k\) 的对称性(甚至由于每次抽球后要进行随机化处理,即使机器人知道其它试验(抽取)情况的任何信息也成立)。这使我们知道,在 \(n\) 次试验(抽取)中恰好取出 \(r\) 个红球的概率与顺序无关,该概率是
(注意,这里并没有要求 \(N\rightarrow + \infty\) )
这就是我们之前在 2.1节 二项分布 中提到的二项分布。在包含有限的 \(N\) 个球的坛子中进行有放回的随机化抽样,具有与无放回抽样在取极限 \(N\rightarrow +\infty\) 时大致相同的效果。
对于较小的 \(n\) 来说,这个近似非常好。但是对于较大的 \(n\) 来说,这些小的误差会累积(具体取决于我们怎么摇坛子等因素),最终导致上式具有误导性。下一节我们关于这点来做出分析。
现在我们假设抽取并放回一个红球会略微使得下一次抽取红球的概率增加 \(\epsilon > 0\) 。抽取并放回一个白球会略微使得下一次抽取白球的概率降低 \(\delta > 0\) 。这里的影响只具备“单步记忆”性,更早的抽取影响相比之下可忽略不计。在某种意义上,可以将此效应称为一种小的“倾向性”,它表达了一种在时间上向前作用的物理因果关系。那么,令 \(C\) 表示上述所有背景信息(包括相关性陈述),记 \(p\equiv M / N\) ,我们有
现在我们考虑上述的相关性如何影响我们在 1.1节:前向推断 中得到的一些计算结果。给定初始状态 \(P(R_1\mid C) = M / N = p, P(W_1\mid C) = (N - M) / N = 1 - p\) ,我们需要递推的求出 \(P(R_2\mid C), P(W_2\mid C), \cdots, P(R_k\mid C), P(W_k\mid C)\) 。递推的计算公式遵循乘法规则:
这定义了一个概率的 马尔可夫链(Markov chain) 。我们将第 \(k\) 次试验的概率写成向量形式
那么上述迭代过程可以使用矩阵表示:
这样,递推过程的计算就可以立即执行到我们需要的任意步:
因此,要获得一般都解,我们只需要找到 \(\boldsymbol{M}\) 的特征值和特征向量即可。 \(\boldsymbol{M}\) 的特征多项式为
\(C(\lambda)= 0\) 的根为特征值 \(\lambda_1 = 1, \lambda_2 = \epsilon + \delta\) 。
已知二级结论:对特征值为 \(\lambda\) 的任意 \(2\times 2\) 矩阵 \(\boldsymbol{M} = \left(\begin{matrix} a & b \\ c & d \end{matrix}\right)\) ,对应的(未归一化)特征向量为 \(\boldsymbol{x}=\left(\begin{matrix} b\\ \lambda - a \end{matrix}\right)\) (关于这个结论大家可自行代入 \(\boldsymbol{M}\boldsymbol{x}=\lambda \boldsymbol{x}\) 验证,就是需要注意最后需要用到特征多项式 \(\lambda^2 - (a + d)\lambda + ad - bc = 0\) 来代换掉 \(ad-bc\) 的值进行化简)。
这样,将 \(\lambda_1, \lambda_2\) 代入,就得到了我们的特征向量
因为 \(\boldsymbol{M}\) 不是对称矩阵,所以上述特征向量不是正交的。不过,如果使用上述特征向量做为一组基底,我们仍然可以对矩阵 \(\boldsymbol{M}\) 进行对角化。令
运用公式 \(\boldsymbol{A}^{-1} = \frac{1}{\mathrm{det}(\boldsymbol{A})}\left(\begin{matrix} A_{22} & - A_{12}\\ -A_{21} & A_{11} \end{matrix}\right)\) (或者高斯消元法)求得其逆为 \(\boldsymbol{S}^{-1}=\frac{1}{1-\epsilon - \delta}\left(\begin{matrix} 1 & 1 \\ q - \epsilon & -(p-\delta) \end{matrix}\right)\) ,于是我们可以对矩阵 \(\boldsymbol{M}\) 进行对角化:
其中 \(\boldsymbol{\Lambda}\) 是对角矩阵。那么,对于任意 \(r\) (无论是正数、负数甚至复数),有
由于对角矩阵 \(\boldsymbol{\Lambda}^r = \left(\begin{matrix} \lambda_1^r & 0 \\ 0 & \lambda_2^r \end{matrix}\right)\) ,于是
又因为 \(\boldsymbol{v_1} = \left(\begin{matrix} p \\ q \end{matrix}\right)\) ,代入 \(\boldsymbol{v}_k = \boldsymbol{M}^{k-1}\boldsymbol{v}_1\) 可得
特别地,当 \(\epsilon = \delta = 0\) 时,上式简化为 \(P(R_k\mid C)=p\) ,这里就得到了我们在 1.1节:前向推断 和 3.1节 随机化与近似:二项分布 中都提到过的结论(尽管当时没有证明)。此时矩阵 \(\boldsymbol{M}=\left(\begin{matrix} p & p \\ 1 - p & 1 - p \end{matrix}\right)\) 为奇异矩阵,回到了已经讨论过的二项分布的情况。
接下来我们来看对于加以相关性校正的马尔可夫链如何进行前向推断(即计算 \(P(R_k\mid R_j B)\) )。在第 \(j\) 次试验中出现红球,那么 \(\boldsymbol{v}_j = \left(\begin{matrix} 1\\ 0 \end{matrix}\right)\) 。根据马尔可夫链的递推公式,我们有
由 \(\boldsymbol{M}^{k-j} = \boldsymbol{S}\boldsymbol{\Lambda}^{k-j}\boldsymbol{S}^{-1}\) 可得
我们发现当 \(|\epsilon + \delta| < 1\) 且 \(k\rightarrow +\infty\) 时,它和 \(P(P_k\mid C)\) 都会趋近于 \((p - \delta) / (1 - \epsilon - \delta)\) 。
那么我们在进行后向推断时,是否还可以使用对称性 \(P(R_j\mid R_k C) = P(R_k\mid R_j C)\) 呢?根据乘法规则,我们有
由于我们已经知道 \(P(R_k\mid C) \neq P(R_j\mid C)\) ,所以
可见后向推断虽然仍然是可能的,但无法再像前向推断那样具有相同的公式。
该示例是一个常见且重要的物理问题的最简单版本:马尔可夫近似中的 不可逆过程(irreversible process) 。另一个常见的技术术语是 一阶自回归模型(autoregressive model of first order) 。
关于坛子模型的适用范围
在大多数实验中,我们并不从真正的“坛子”中抽取球。然而,“伯努利坛子”已被证明是一种有用的概念工具。但是某些人可能对“坛子”一词感到不悦。因此,在许多文献中人们会发现诸如“从总体中抽取”这样的说法。
在诸如抽样调查、工业质量控制检测等场景中,人们真的是从 有限 的真实总体中抽取结果的,坛子的类比其实非常合适,本章所提到的概率分布都适用。然而对于抛硬币、测量温度和风速、预测商品价格等场景,坛子的类比就很牵强了。然而在许多文献中,人们仍然使用坛子分布来表示数据的概率,并试图通过将实验视为从某种“假设的 无限 总体”中抽取来证明这一选择的合理性,而这完全是他们的臆造之物。因为在真实情况下,我们不能保证连续的抽取都是严格独立的。坛子类型的概念化只能处理最原始的信息,而真正复杂的应用要求我们发展出远远超出坛子模型的原理。总之,在接下来的应用中,必须考虑实验是否真的与从坛子中抽取球类似。
抽样分布绝不是终点
本章中发现的概率分布称为 抽样分布(sampling distributions) ,或称 直接概率(direct probability) 。所谓直接概率,是指给定关于所观察现象的假设 \(H\) ,数据 \(D\) 的概率分布 \(p(D \mid H)\) ,与 逆概率(inverse probability) 即对应假设的分布 \(p(H \mid D)\) 相对。在本文的伯努利坛子模型中,假设 \(H\) 即坛子的内容 \((M, N)\) ,数据 \(D\) 即所生成的红球和白球的序列。
抽样分布为我们提供了可能观测结果的预测(例如 \(r\) 的不同可能值及其对应的概率)。抽样分布的预测结果与实际观察结果的差别大小,为我们接收或拒绝当前假设提供了合理的依据,并用于寻找新的假设,这是 显著性检验(significance tests) 的主题。
尽管抽样理论在传统概率论教学中占主导地位,但在现实世界中,此类问题几乎可以忽略不计。在几乎所有科学推断的实际问题中,我们都处在相反的境地:数据 \(D\) 是已知的,但正确的假设是未知的。此时我们面临的是 逆问题(inverse problem) :如何求概率分布 \(p(H\mid D)\) ?因此,在接下来的章节中,我们的注意力将几乎全部集中在解决这种逆问题的方法上。当然,计算抽样分布仍然是我们工作的组成部分之一,但它绝不是终点。
热门资讯